Some time ago I had met at my work with an interesting problem. I was working for a construction company, in the warehouses, managers order different size tubes which are divided into smaller parts called panels. Panels have different lengths as well but always less than a length of tubes. To construct a building, the company needs to create a lot of panels which are obtained by cutting tubes. The leftover tubes cannot be combined with each other, hence, the rest of the used tube will be less than the smaller required panel it must be thrown away (so-called a scrap). Utilization of scrap is costly, so production excessive scrap is unfavorable.
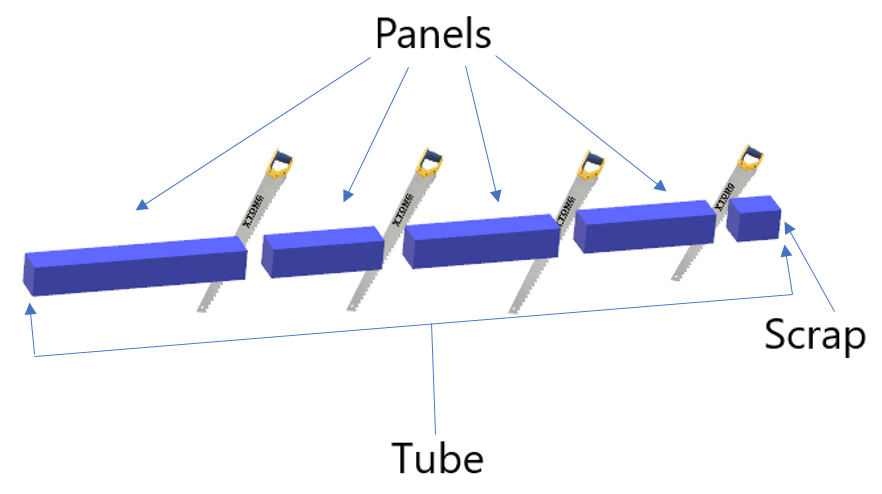
What are the problems?
- What length of tubes do managers need to order so that scrap amount will be as low as possible?
- How to cut ordered tubes to get all the required panels?
Perhaps you guessed it! The problem is strongly related to the ‘bin packing problem’ but with a significant difference – containers (bins) can have a variable size. Unfortunately, the problem is not easy to fix, moreover, it belongs to NP-hardness class of problem.
How can it be resolved? I think there are many solutions, some are effective, others are time-consuming. I will try to quickly describe several of them.
Deep learning
One of the solutions is described here.
Heuristics
- J.Kang, S.Park, Algorithms for the variable sized bin packing problem
- M.Maiza, A.Labed M.S. Radjef, Efficient algorithms for the offline variable sized bin-packing problem
A simple case using only one length of the tube
If we choose only one length of tube (preferable, the longest), an unusual bin packing problem will start to occur with one exception – the last packing phase will select the shortest possible tube.
I recommend trying to implement one of above solution and test it using cases where usual bin packing algorithm does not return optimal results.


Leave a Reply